Conditional Probability and Bayes Theorem
Published:
This post covers Introduction to probability from Statistics for Engineers and Scientists by William Navidi.
Basic Ideas
Conditional Probability and Independence
A probability that is based on a part of a sample space is called a conditional probability.
The key to computing the probability is to realize that knowledge - the condition that meets the specification reduces the sample space.
Let $A$ and $B$ be events with $P(B) \ne 0$.
The conditional probability of A given B is:
$ P(A \mid B) = \frac{P(A ∩ B)}{P(B)} $

What is the probability that a randomly selected person is male, given that they own a pet?
| Do not have pets | Have pets | Total | |
|---|---|---|---|
| Male | 0.08 | .41 | .49 |
| Female | 0.06 | .45 | .51 |
| Total | 0.14 | .86 | 1 |
Independent Events
Sometimes the knowledge that one event has occurred does not change the probability that another event occurs.
In this case the conditional and unconditional probabilities are the same, and the events are said to be independent
Two events A and B are independent if the probability of each event remains the same whether or not the other occurs. In symbols:
- If $P(A) \ne 0$ and $P(B) \ne 0$, then $A$ and $B$ are independent if
- $P(B \mid A) = P(B)$ or, equivalently, $P(A \mid B) = P(A)$.
- If either $P(A) = 0$ or $P(B) = 0$, then $A$ and $B$ are independent.
Events $A_{1}, A_{2}\ldots A_{n}$ are independent if the probability of each remains the same no matter which of the others occur. In symbols:
Events $A_{1}, A_{2} \ldots A_n$ are independent if for each $A_i$, and each collection $A_{j1},…, A_{jm}$ of events with $P(A_{j1} \cap \ldots \cap A _{jm}) ≠ 0$,
$P(A_{i} \mid A_{j1} \cap \ldots \cap A_{jm}) = P(A_i)$
A system contains two components, A and B. Both components must function for the system to work. The probability that component A fails is $0.08$, and the probability that component B fails is $0.05$. Assume the two components function independently. What is the probability that the system functions?
The Multiplication Rule
If $A$ and $B$ are two events with $P(B) \ne 0$, then $P(A \cap B) = P(B)P(A \mid B) $
If $A$ and $B$ are two events with $P(A) \ne 0$, then $P(A \cup B) = P(A)P(B \mid A)$
The Law of Total Probability
A sample space contains the events A1, A2, A3, and A4. They are also exhaustive, which means that their union covers the whole sample space.
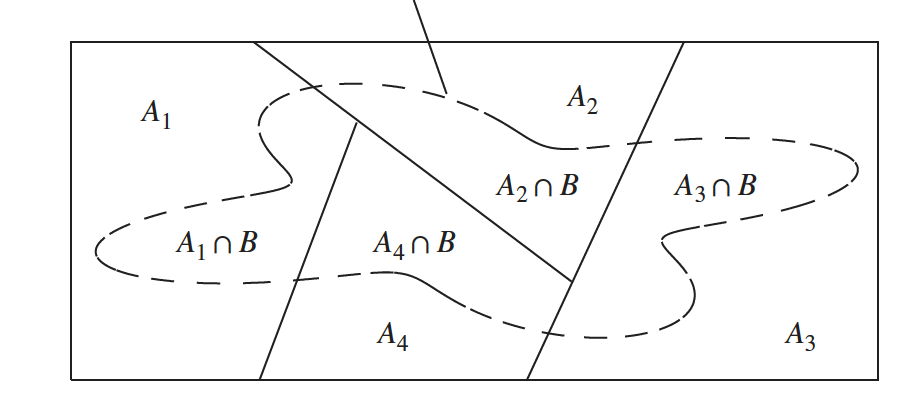
The mutually exclusive and exhaustive events $A_{1}, A_{2}, A_{3}, A_{4}$ divide the event $B$ into mutually exclusive subsets.
If $A_{1} \ldots A_{n}$ are mutually exclusive and exhaustive events, and B is any event, then $P(B) = P(A_{1} \cap B) + \ldots + P(A_{n} \cap B)$
Equivalently,
if $P(A_{i}) \ne 0$ for each $A_{i}$,
$P(B) = P(B \mid A_{1})P(A_{1}) + \ldots + P(B \mid A_{n})P(A_{n})$
Customers who purchase a certain make of car can order an engine in any of three sizes. Of all cars sold, $45\%$ have the smallest engine, 35% have the medium-sized one, and $20\%$ have the largest. Of cars with the smallest engine, $10\%$ fail an emissions test within two years of purchase, while $12\%$ of those with the medium size and $15\%$ of those with the largest engine fail. What is the probability that a randomly chosen car will fail an emissions test within two years?
Bayes’ Rule
Let $A_{1},…, A_{n}$ be mutually exclusive and exhaustive events with $P(Ai) \ne 0$ for each $A_{i}$. Let $B$ be any event with $P(B) \ne 0$. Then $ P(A_{k} \mid B) = P(B \mid A_{k})P(A_{k}) $ where $\Sigma n_{i} =1$ and $P(B \mid A_{i})P(A_{i})$
Special Case- Let A and B be events with $P(A) ≠ 0$, $P(A ^{c}) ≠ 0$, and P(B) ≠ 0. Then
$P(A \mid B) = \frac{ P(B \mid A)P(A)}{ P(B \mid A)P(A) + P(B \mid A^{c})P(A^{c})}$
A man is known to speak the truth 2 out of 3 times. He throws a die and reports that the number obtained is a four. Find the probability that the number obtained is actually a four.
Application to Reliability Analysis
- Reliability analysis is the branch of engineering concerned with estimating the failure rates of systems
- Problem: A production method used in the manufacture of aluminum cans. The following schematic diagram, slightly simplified, depicts the process. The initial input into the process consists of coiled aluminum sheets, approximately $0.25 mm$ thick. In a process known as “cupping,” these sheets are uncoiled and shaped into can bodies, which are cylinders that are closed on the bottom and open on top. These can bodies are then washed and sent to the printer, which prints the label on the can. In practice there are several printers on a line; the diagram presents a line with three printers. The printer deposits the cans onto pallets, which are wooden structures that hold $7140$ cans each. The cans next go to be filled. Some fill lines can accept cans directly from the pallets, but others can accept them only from cell bins, which are large containers holding approximately $100,000$ cans each. To use these fill lines, the cans must be transported from the pallets to cell bins, in a process called depalletizing. In practice there are several fill lines; the diagram presents a case where there are two fill lines, one of which will accept cans from the pallets, and the other of which will not. In the filling process the cans are filled, and the can top is seamed on. The cans are then packaged and shipped to distributors. It is desired to estimate the probability that the process will function for one day without failing. Assume that the cupping process has probability $0.995$ of functioning successfully for one day. Since this component is denoted by $A$ in the diagram, we will express this probability as $P(A) = 0.995$. Assume that the other process components have the following probabilities of functioning successfully during a oneday period: $P(B) = 0.99, P(C) = P(D) = P(E) = 0.95, P(F) = 0.90, P(G) = 0.90, P(H) = 0.98.$ Assume the components function independently. Find the probability that the process functions successfully for one day.
