This post covers Introduction to probability from Statistics for Engineers and Scientists by William Navidi.

Basic Ideas

• Experiment

  • a process that results in an outcome that cannot be predicted in advance with certainty.
    • Tossing a coin
    • rolling a die
    • measuring the diameter of a bolt
    • weighing the contents of a box of cereal
    • measuring the breaking strength of a length of fishing line

• Sample Space

  • The set of all possible outcomes of an experiment is called the sample space for the experiment
    • Finite
      • Tossing a coin: {Heads, Tails}
      • Rolling six-sided die: ${1, 2, 3, 4, 5, 6}$
    • Infinite
      • Punch with diameter $10 mm$ punches holes in sheet metal
        • May vary $10.0$ and $10.2 mm$
          • variations in the angle of the punch
          • slight movements in the sheet metal
        • Reasonable sample space is the interval $(10.0, 10.2)$ - infinite
    • Finite or Infinite
      • Process manufactures steel pins whose lengths vary between $5.20$ and $5.25$ cm.
      • Sample space: ${x \mid 5.20 < x < 5.25}$.
      • Sample space: {too short, too long, within specifications}
        • if the object were simply to determine whether the pin was too short, too long, or within specification limits

• Event

  • A subset of a sample space is called an event
    • probability that a die comes up an even number
    • Empty set is an event, $\phi$
    • Set itself is an event
    • A given event is said to have occurred if the outcome of the experiment is one of the outcomes in the event.
      • if a die comes up 2,
        • the events ${2, 4, 6}$ and ${1, 2, 3}$ have both occurred

• An electrical engineer has on hand two boxes of resistors, with four resistors in eachbox. The resistors in the first box are labeled $10 Ω (ohms)$, but in fact their resistances are $9$, $10$, $11$, and $12 Ω$. The resistors in the second box are labeled $20 Ω$, but in fact their resistances are $18$, $19$, $20$, and $21 Ω$. The engineer chooses one resistor from each box and determines the resistance of each. Let $A$ be the event that the first resistor has a resistance greater than $10$, let $B$ be the event that the second resistor has a resistance less than $19$, and let $C$ be the event that the sum of the resistances is equal to $28$. Find a sample space for this experiment, and specify the subsets corresponding to the events $A$, $B$, and $C$.

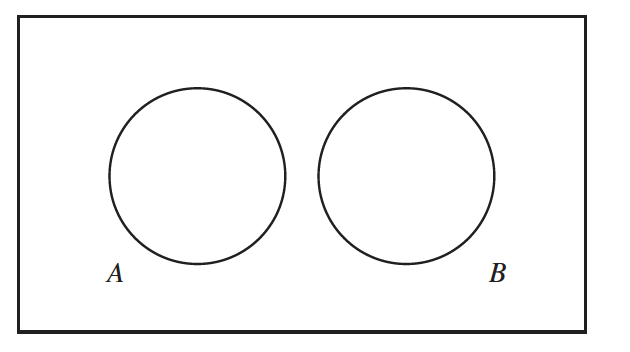
• Mutually Exclusive Events

  • The events A and B are said to be mutually exclusive if they have no outcomes in common.

• The Axioms of Probability
  • Let S be a sample space. Then P(S) = 1.
  • For any event $A$, $0 ≤ P(A) ≤ 1$.

  • If $A$ and $B$ are mutually exclusive events, then $P(A \cup B) = P(A) + P(B)$.

  • More generally, if $A_{1}, A_{2},\ldots$ are mutually exclusive events, then
    • $P(A_{1} \cup A_{2} \ldots) = P(A_{1}) + P(A_{2}) + \ldots$.

• Sample Spaces with Equally Likely Outcomes

  • A population from which an item is sampled at random can be thought of as a sample space with equally likely outcomes

  • If S is a sample space containing N equally likely outcomes, and if $A$ is an event containing k outcomes, then $P(A) = \frac{k}{N}$

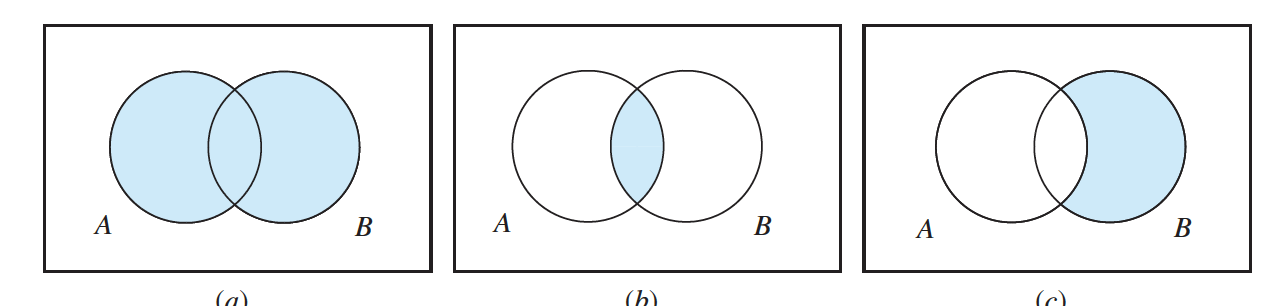
  • Let A and B be any events. Then $P(A \cup B) = P(A) + P(B) − P(A \cap B)$

• In a process that manufactures aluminum cans, the probability that a can has a flaw on its side is $0.02$, the probability that a can has a flaw on the top is $0.03$, and the probability that a can has a flaw on both the side and the top is $0.01$. What is the probability that a randomly chosen can has a flaw? What is the probability that it has no flaw?

Theorem1: Prove that $P(\hat A) = 1 − P(A)$

Proof: Let $S$ be a sample space and let $A$ be an event. Then $A$ and $\hat{A}$ are mutually exclusive, so by Axiom 3,

$P(A ∪ \hat{A}) = P(A) + P(\hat{A})$

But $A \cup \hat{A} = S$, and by Axiom 1, $P(S) = 1$. Therefore

$P(A ∪ \hat A) = P(S) = 1$

It follows that $P(A) + P(\hat A) = 1, so ~ P(\hat A) = 1 − P(A)$.

Theorem2: Prove that $P(\phi) = 0$

Proof: Let $S$ be a sample space. Then $\phi = \hat S$. Therefore $P(\phi) = 1 − P(S) = 1 − 1 = 0$.

$ A \cup B = A \cap \hat B + A \cap B + \hat A \cap B $ ​
$ A = (A \cup \hat B) \cup (A \cap B) $
$ B = (\hat A \cap B) \cup (A \cap B) $

Theorem3: Prove that $P(A \cup B) = P(A) + P(B) − P(A \cap B)$​

Proof: $P(A \cup B) = P(A \cap \hat B) + P(A \cap B) + P(\hat A \cap B) $​

Now $A = (A \cup \hat B) \cup (A \cap B), ~and~ B = (\hat A \cap B) \cup (A \cap B)$​​.

Therefore, $P(A) = P(A \cap \hat B) + P(A \cap B)$​ and $P(B) = P(\hat A \cap B) + P(A \cap B)$

Summing above Equations $P(A)$​ and $P(B)$​​ yields \(\begin{align} P(A) + P(B) &= P(A \cap \hat B) + P(\hat A \cap B) + 2P(A \cap B) \\ &= P(A \cap \hat B) + P(\hat A \cap B) + P(A \cap B) + P(A \cap B) \\ &= P(A \cup B) + P(A \cap B) \end{align}\) It follows that $P(A \cup B) = P(A) + P(B) − P(A \cap B)$.