This post covers WIRELESS COMMUNICATIONS AND NETWORKS by William Stallings.

Basic Ideas

• Code Division Multiple Access (CDMA)

• CDMA is a multiplexing technique used with spread spectrum.
• We start with a data signal with rate D, which we call the bit data rate.
• We break each bit into k chips according to a fixed pattern that is specific to each user called the user’s code.
• The new channel has a chip data rate of kD chips per second.
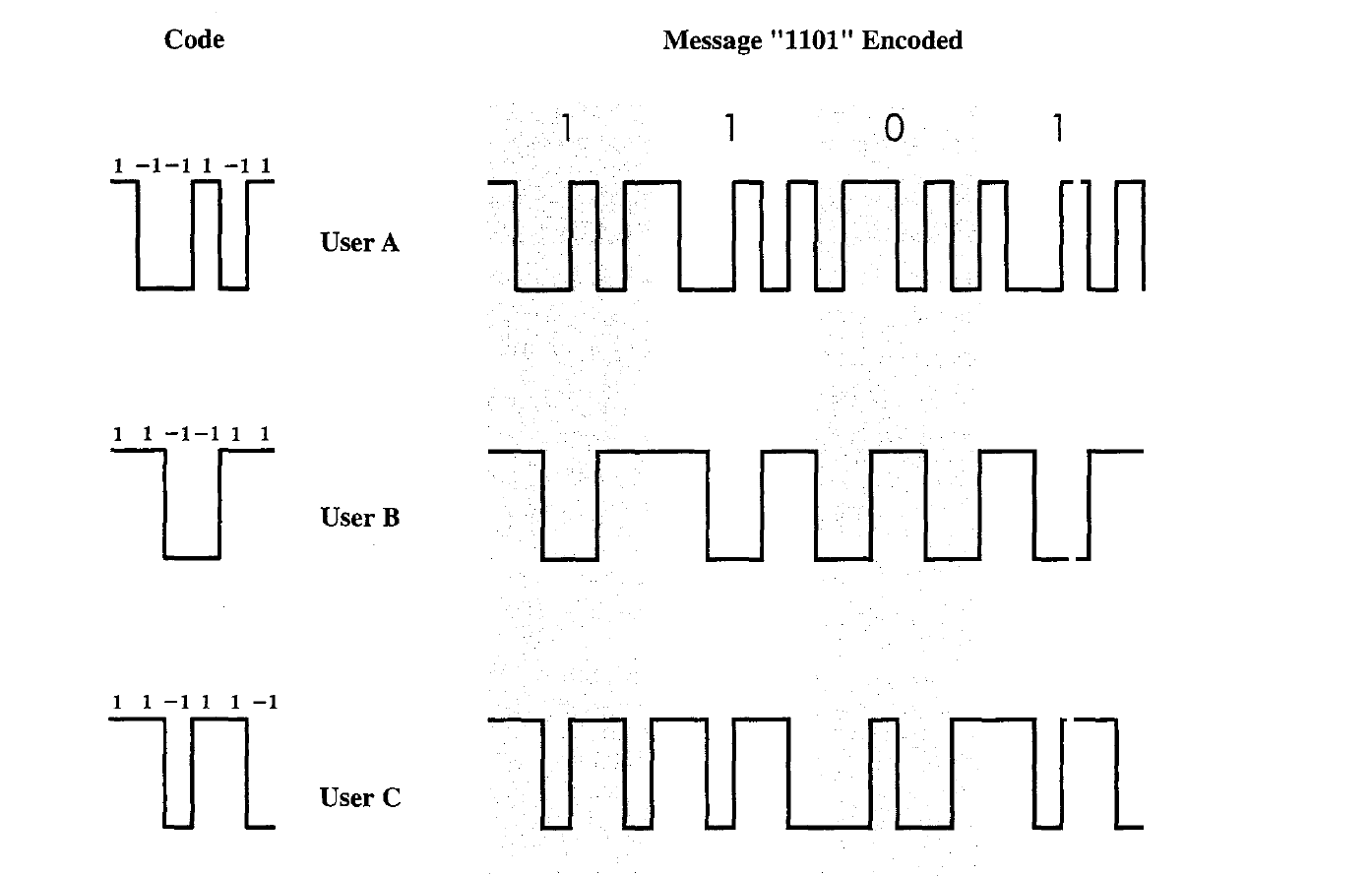
• As an illustration we consider a simple example with k = 6. It is simplest to characterize a code as a sequence of Is and -Is.
• Let three users, A, B, and C, each of which is communicating with the same base station receiver, R.
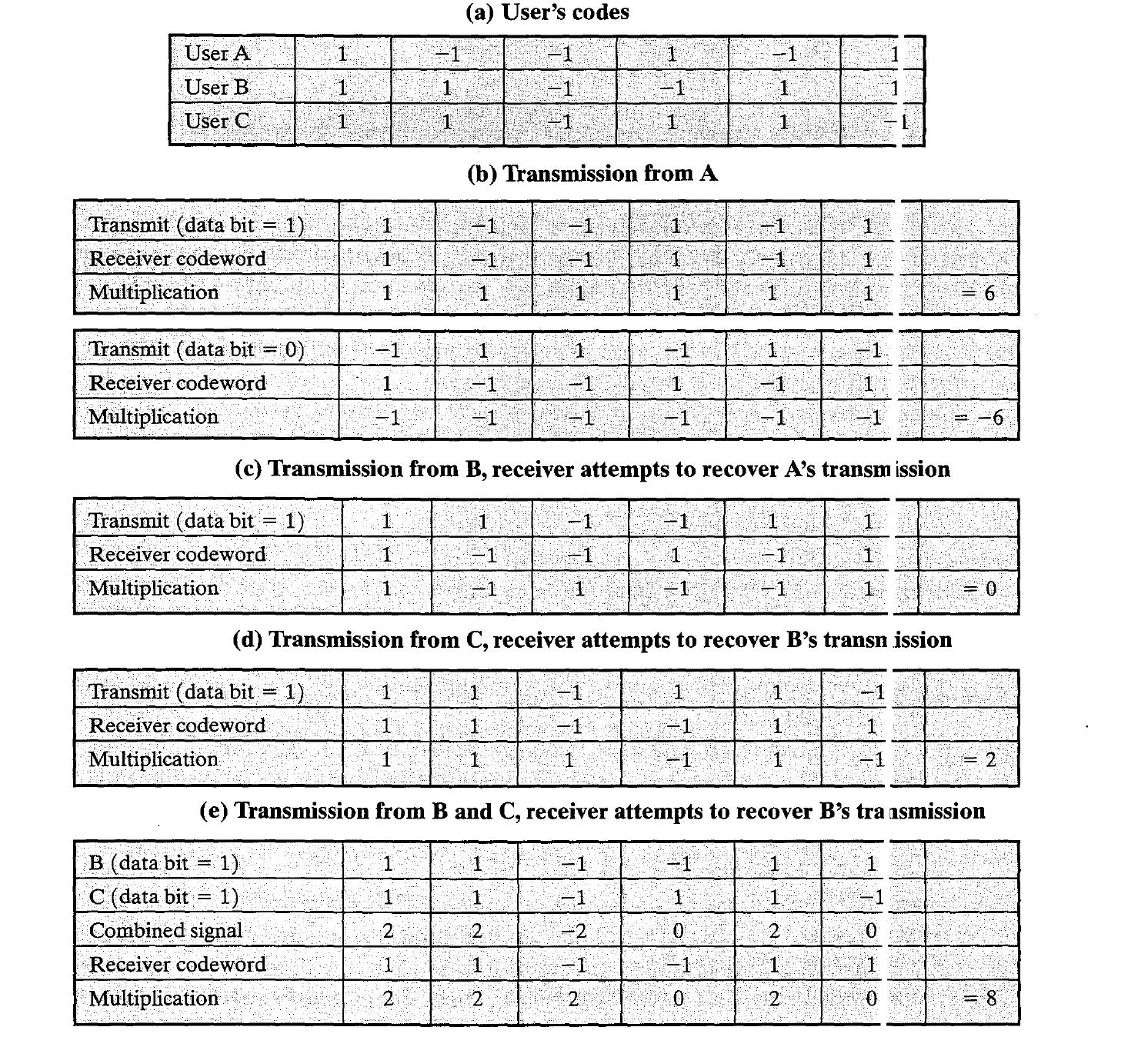
• Thus, the code for user A is $C_A = <1, -1, -1,1, -1,1>$. Similarly, user B has code $C_B = <1,1,-1, -1, 1, 1>$, and user C has $C_c = <1,1, -1,1, 1, -1>$.
• We now consider the case of user A communicating with the base station. The base station is assumed to know A’s code.
• For simplicity, we assume the communication is already synchronized so that the base station knows when to look for codes.
• If A wants to send a 1 bit, A transmits its code as a (chip pattern $<1, -1, -1,1, -1,1>$. If a 0 bit is to be sent, A transmits the complement (1s and -1s reversed) of its code, $<-1,1,1, -1, 1, -1>$.
• At the base station the receiver decodes the chip patterns. In our simple version, if the receiver R receives a chip pattern $d = <d_1, d_2, d_3, d_4, d_5, d_6>$, and the receiver is seeking to communicate with a user u so that it has at hand u’s code, $<c_l, c_2, c_3, c_4, c_5, c_6>$, the receiver performs electronically the following decoding function:

• Please note that it is always the case that $-6 \leq S_A(d) \leq 6$ no matter what sequence of -1s and 1s comprised, and that the only values of d resulting in the extreme values of 6 and -6 are A’s code and its complement, respectively.
• So if $S_A$ produces a +6, we say that we have received a 1 bit from A; if $S_A$ produces a -6, we say that we have received a 0 bit from user A; otherwise, we assure that someone else is sending information or there is an error.
• So why go through all this? The reason becomes clear if we see what happens if user B is sending and we try to receive it with $S_A$, that is, we are decoding with the wrong code, A’s.
• If B sends a 1 bit, then $d = <1,1, -1, -1, 1, 1>$. Then it with $S_A$, that is, we are decoding with the wrong code, A’s. If B sends a 1 bit, then $d = <1,1, -1, -1, 1, 1>$. Then

• Thus, the unwanted signal (from B) does not show up at all. Yo II can easily verify that if B had sent a 0 bit, the decoder would produce a value of 0 for $S_A$ again.
• This means that if the decoder is linear and if A and B transmit signals ‘A and SB, respectively, at the same time, then $S_A(S_A + S_B) = S_A(S_A) + S_A(S_B) = S_A(S_A)$ since the decoder ignores B when it is using A’s code.
• The codes of A and B that have the property that $S_A(C_B) = S_B( C_A) = 0$ are called orthogonal.
• Such codes are very nice to have but there are not all that many of them. More common is the case when $S_x( C_y)$ is small in absolute value when $X \times Y$.
• Then it is easy to distinguish between the two cases when X = Y and when X =Y. In our example $S_A(c_d = S_c(C_A) = 0$, but $S_B(c_d = S_dC_B) = 2$.
• In the latter case the C signal would make a small contribution to the decoded signal instead of O.
• Using the decoder, $S_u$, the receiver can sort out transmission from u even when there may be other users broadcasting in the same cell.
• Table summarizes the example from the preceding discussion. In practice, the CDMA receiver can filter out the contribution from unwanted users or they appear as low-level noise.
• However, if there are mainly users competing for the channel with the user the receiver is trying to listen to, or if the signal power of one or more competing signals is too high, perhaps because it is very near the receiver (the “near/far” problem), the system breaks down.

• CDMA for Direct Sequence Spread Spectrum
• Let us now look at CDMA from the viewpoint of a DSSS system llsing BPSK.
• Figure depicts a configuration in which there are n users, each transmitting using a different, orthogonal, PN sequence.
• For each user, the data stream to be transmitted, $d_i(t)$, is BPSK modulated to produce a signal with a bandwidth of $W_s$ and then multiplied by the spreading code for that user, $C_i(t)$. All of the signals, plus noise, are received at the receiver’s antenna.
• Suppose that the receiver is attempting to recover the data of user 1.
• The incoming signal is multiplied by the spreading code of user 1 and then demodulated.
• The effect of this is to narrow the bandwidth of that portion of the incoming signal corresponding to user 1 to the original bandwidth of the unspread signal, which is proportional to the data rate.
• Because the remainder of the incoming signal is orthogonal to the spreading code of user 1, that remainder still has the bandwidth $W_s$. Thus the unwanted signal energy remains spread over a large bandwidth and the wanted signal is concentrated in a narrow bandwidth.
• The bandpass filter at the demodulator can therefore recover the desired signal.