Capacity And Cell Coverage
Published:
This post covers Wireless Communications: Principles and Practices by Theodore S. Rapport.
Basic Ideas
The Cellular Concept- Fundamental System Design
Capacity And Cell Coverage
Previously, we have seen that the frequency reuse technique in cellular systems allows for almost boundless expansion of geographical area and the number of mobile system users who could be accommodated.
In designing a cellular layout, the two parameters which are of great significance are the cell radius R and the cluster size N, and we have also seen that co-channel cell distance $D = \sqrt{3N}R$.
In the following, a brief description of the design trade-off is given, in which the above two parameters play a crucial role.
The cell radius governs both the geographical area covered by a cell and also the number of subscribers who can be serviced, given the subscriber density.
It is easy to see that the cell radius must be as large as possible.
This is because, every cell requires an investment in a tower, land on which the tower is placed, and radio transmission equipment and so a large cell size minimizes the cost per subscriber.
Eventually, the cell radius is determined by the requirement that adequate signal to noise ratio be maintained over the coverage area.
The SNR is determined by several factors such as the antenna height, transmitter power, receiver noise gure etc. Given a cell radius $R$ and a cluster size $N$, the geographic area covered by a cluster is
$A_{cluster} = NA_{cell} = \frac{N3 \sqrt{3}R^2}{2}$
If the total serviced area is $A_{total}$, then the number of clusters M that could be accommodated is given by \(M = \frac{A_{total}}{A_{cluster}}\)
Note that all of the available channels $N$, are reused in every cluster. Hence, to make the maximum number of channels available to subscribers, the number of clusters M should be large, which, by above Equation, shows that the cell radius should be small.
However, cell radius is determined by a trade-off: R should be as large as possible to minimize the cost of the installation per subscriber, but R should be as small as possible to maximize the number of customers that the system can accommodate.
Now, if the cell radius $R$ is fixed, then the number of clusters could be maximized by minimizing the size of a cluster $N$.
We have seen earlier that the size of a cluster depends on the frequency reuse ratio $Q$.
Hence, in determining the value of $N$, another trade-off is encountered in that $N$ must be small to accommodate large number of subscribers, but should be sufficiently large so as to minimize the interference effects.
Now, we focus on the issues regarding system expansion. The history of cellular phones has been characterized by a rapid growth and expansion in cell subscribers.
Though a cellular system can be expanded by simply adding cells to the geographical area, the way in which user density can be increased is also important to look at.
This is because it is not always possible to counter the increasing demand for cellular systems just by increasing the geographical coverage area due to the limitations in obtaining new land with suitable requirements.
We discuss here two methods for dealing with an increasing subscriber density: Cell Splitting and Sectoring. The other method, microcell zone concept can treated as enhancing the $QoS$ in a cellular system.
The basic idea of adopting the cellular approach is to allow space for the growth of mobile users.
When a new system is deployed, the demand for it is fairly low and users are assumed to be uniformly distributed over the service area.
However, as new users subscribe to the cellular service, the demand for channels may begin to exceed the capacity of some base stations.
As discussed previously, the number of channels available to customers (equivalently, the channel density per square kilo meter) could be increased by decreasing the cluster size.
However, once a system has been initially deployed, a system-wide reduction in cluster size may not be necessary since user density does not grow uniformly in all parts of the geographical area.
It might be that an increase in channel density is required only in specific parts of the system to support an increased demand in those areas.
Cell-Splitting : is a technique which has the capability to add new smaller cells in specific areas of the system.
Cell Splitting is based on the cell radius reduction and minimizes the need to modify the existing cell parameters.
Cell splitting involves the process of sub-dividing a congested cell into smaller cells, each with its own base station and a corresponding reduction in antenna size and transmitting power.
This increases the capacity of a cellular system since it increases the number of times that channels are reused.
Since the new cells have smaller radii than the existing cells, inserting these smaller cells, known as microcells, between the already existing cells results in an increase of capacity due to the additional number of channels per unit area.
There are few challenges in increasing the capacity by reducing the cell radius.
Clearly, if cells are small, there would have to be more of them and so additional base stations will be needed in the system.
The challenge in this case is to introduce the new base stations without the need to move the already existing base station towers.
The other challenge is to meet the generally increasing demand that may vary quite rapidly between geographical areas of the system.
For instance, a city may have highly populated areas and so the demand must be supported by cells with the smallest radius.
The radius of cells will generally increase as we move from urban to sub urban areas, because the user density decreases on moving towards sub-urban areas.
The key factor is to add as minimum number of smaller cells as possible
wherever an increase in demand occurs. The gradual addition of the smaller cells implies that, at least for a time, the cellular system operates with cells of more than one size.

Figure shows a cellular layout with seven-cell clusters. Consider that the cells in the center of the diagram are becoming congested, and cell
A in the center has reached its maximum capacity. Figure also shows how the smaller cells are being superimposed on the original layout. The new smaller cells have half the cell radius of the original cells.
At half the radius, the new cells will have one-fourth of the area and will consequently need to support one-fourth the number of subscribers.
Notice that one of the new smaller cells lies in the center of each of the larger cells.
If we assume that base stations are located in the cell centers, this allows the original base stations to be maintained even in the new system layout.
However, new base stations will have to be added for new cells that do not lie in the center of the larger cells.
The organization of cells into clusters is independent of the cell radius, so that the cluster size can be the same in the small-cell layout as it was in the large-cell layout.
Also the signal-to-interference ratio is determined by cluster size and not by cell radius. Consequently, if the cluster size is maintained, the signal-to-interference ratio will be the same after cell splitting as it was before.
If the entire system is replaced with new half-radius cells, and the cluster size is maintained, the number of channels per cell will be exactly as it was before, and the number of subscribers per cell will have been reduced.
When the cell radius is reduced by a factor, it is also desirable to reduce the transmitted power.
The transmit power of the new cells with radius half that of the old cells can be found by examining the received power PR at the new and old cell boundaries and setting them equal.
This is necessary to maintain the same frequency re-use plan in the new cell layout as well.
Assume that $P_{T1}$ and $P_{T_2}$ are the transmit powers of the larger and smaller base stations respectively.
replaced with new half-radius cells, and the cluster size is maintained, the number of channels per cell will be exactly as it was before, and the number of subscribers per cell will have been reduced.
When the cell radius is reduced by a factor, it is also desirable to reduce the transmitted power.
The transmit power of the new cells with radius half that of the old cells can be found by examining the received power $P_R$ at the new and old cell boundaries and setting them equal.
This is necessary to maintain the same frequency re-use plan in the new cell layout as well.
Assume that $P_{T1}$ and $P_{T2}$ are the transmit powers of the larger and smaller base stations respectively.
Then, assuming a path loss index $n=4$, we have power received at old cell boundary = $P_{T1}=R^4$ and the power received at new cell boundary = $P_{T2}/(R/2)^4$.
On equating the two received powers, we get $P_{T2} = P_{T1} / 16$.
In other words, the transmit power must be reduced by $12 dB$ in order to maintain the same $S/I$ with the new system lay-out.
At the beginning of this channel splitting process, there would be fewer channels in the smaller power groups.
As the demand increases, more and more channels need to be accommodated and hence the splitting process continues until all the larger cells have been replaced by the smaller cells, at which point splitting is complete within the region and the entire system is rescaled to have a smaller radius per cell.
If a cellular layout is replaced entirety by a new layout with a smaller cell radius, the signal-to-interference ratio will not change, provided the cluster size does not change.
Some special care must be taken, however, to avoid co-channel interference when both large and small cell radii coexist.
It turns out that the only way to avoid interference between the large-cell and small-cell systems is to assign entirely different sets of channels to the two systems.
So, when two sizes of cells co-exist in a system, channels in the old cell must be broken down into two groups, one that corresponds to larger cell reuse requirements and the other which corresponds to the smaller cell reuse requirements.
The larger cell is usually dedicated to high speed users as in the umbrella cell approach so as to minimize the number of hand-offs.
Sectoring: Sectoring is basically a technique which can increase the $SIR$ without necessitating an increase in the cluster size.
Till now, it has been assumed that the base station is located in the center of a cell and radiates uniformly in all the directions behaving as an omni-directional antenna.
However it has been found that the co-channel interference in a cellular system may be decreased by replacing a single omni-directional antenna at the base station by several directional antennas, each radiating within a specied sector.
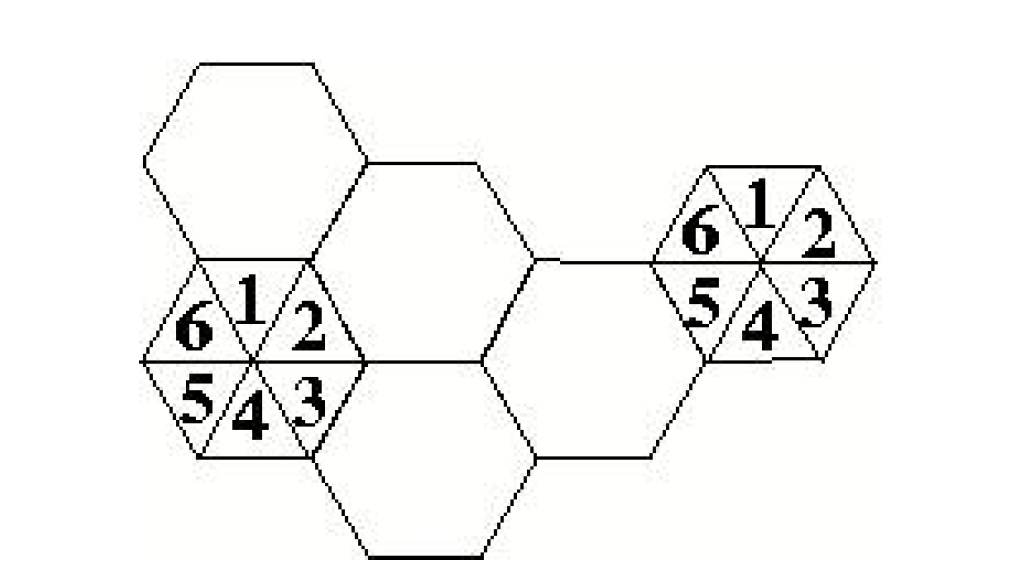
In the Figure, a cell is shown which has been split into three $120^o$ sectors. The base station feeds three $120^o$ directional antennas, each of which radiates into one of the three sectors.
The channel set serving this cell has also been divided, so that each sector is assigned one-third of the available number cell of channels.
This technique for reducing co-channel interference wherein by using suitable directional antennas, a given cell would receive interference and transmit with a fraction of available co-channel cells is called ‘sectoring’.
In a seven-cell-cluster layout with $120^o$ sectored cells, it can be easily understood that the mobile units in a particular sector of the center cell will receive co-channel interference from only two of the first-tier co-channel base stations, rather than from all six.
Likewise, the base station in the center cell will receive co-channel interference from mobile units in only two of the co-channel cells. Hence the signal to interference ratio is now modified to \(\frac{S}{I} = \frac{(\sqrt{3N})^n}{2}\)
where the denominator has been reduced from $6$ to $2$ to account for the reduced number of interfering sources. Now, the signal to interference ratio for a seven-cell cluster layout using $120^o$ sectored antennas can be found from equation to be $23.4 dB$ which is a significant improvement over the Omni-directional case where the worst-case $S/I$ is found to be $17 dB$ (assuming a path-loss exponent, $n=4$).
Some cellular systems divide the cells into $60^o$ sectors. Similar analysis can be performed on them as well.
The calculations in the above example are actually an idealization for several reasons.
Firstly, practical antennas have side lobes and cannot be used to focus a transmitted beam into a perfect $120^o$ sector or $60^o$ sector. Due to this, additional interference will be introduced.
Next, it is also a cause of concern that a given number of channels are not able to support as many subscribers when the pool of channels is divided into small groups.
This is due to a reduction in Trunking Efficiency, a term which will be explained later on.
Because sectoring involves using more than one antenna per base station, the available channels in the cell are divided and dedicated to a specific antenna.
This breaks the available set of channels into smaller sets, thus reducing the trunking efficiency.
Moreover, dividing a cell into sectors requires that a call in progress will have to be handed o (that is, assigned a new channel) when a mobile unit travels into a new sector.
This increases the complexity of the system and also the load on the mobile switching center/base station.
Question: A cellular system having a seven-cell cluster layout with omni-directional antennas has been performing satisfactorily for a required signal to interference ratio of $15$ dB. However due to the need for increasing the number of available channels, a $60^o$ sectoring of the cells has been introduced. By what percentage can the number of channels N total be increased assuming a path-loss component $n=4$?
Microcell Zone Concept
- The increased number of handoffs required when sectoring is employed results in an increased load on the switching and control link elements of the mobile system.
- To overcome this problem, a new microcell zone concept has been proposed. As shown in Figure, this scheme has a cell divided into three microcell zones, with each of the three zone sites connected to the base station and sharing the same radio equipment.
- It is necessary to note that all the microcell zones, within a cell, use the same frequency used by that cell; that is no handovers occur between microcells.
- Thus when a mobile user moves between two microcell zones of the cell, the BS simply switches the channel to a different zone site and no physical re-allotment of channel takes place.
Trunked Radio System:
Cellular radio systems rely on trunking to accommodate a large number of users in a limited radio spectrum. The concept of trunking allows a large number of users to share the relatively small number of channels in a cell by providing access to each user, on demand, from a pool of available channels.
In a trunked radio system, each user is allocated a channel on a per call basis, and upon termination of the call, the previously occupied channel is immediately returned to the pool of available channels.
Trunking exploits the statistical behavior of users so that a fixed number of channels or circuits may accommodate a large, random user community. The telephone company uses trunking theory to determine the number of telephone
Circuits that need to be allocated for office buildings with hundreds of telephones, and this same principle is used in designing cellular radio systems. There is a trade-off between the number of available telephone circuits and the likelihood of a particular user finding that no circuits are available during the peak calling time.
As the number of phone lines decreases, it becomes more likely that all circuits will be busy for a particular user. In a trunked mobile radio system, when a particular user requests service and all of the radio channels are already in use, the user is blocked, or denied access to the system.
In some systems, a queue may be used to hold the requesting users until a channel becomes available.
To design trunk radio systems that can handle a specific capacity at a specific “grade of service”, it is essential to understand trunking theory and queuing theory
The fundamentals of trunking theory were developed by Erlang, a Danish mathematician who, in the late 19th century, embarked on the study of how a large population could be accommodated by a limited number of servers.
Today, the measure of traffic intensity bears his name. One Erlang represents the amount of traffic intensity carried by a channel that is completely occupied (i.e. 1 call-hour per hour or 1 call-minute per minute).
For example, a radio channel that is occupied for thirty minutes during an hour carries 0.5 Erlangs of traffic.
The grade of service (GOS) is a measure of the ability of a user to access a trunked system during the busiest hour.
The busy hour is based upon customer demand at the busiest hour during a week, month, or year. The busy hours for cellular radio systems typically occur during rush hours, between 4 p.m. and 6 p.m. on a Thursday or Friday evening.
The grade of service is a benchmark used to define the desired performance of a particular trunked system by specifying a desired likelihood of a user obtaining channel access given a specific number of channels available in the system.
It is the wireless designer’s job to estimate the maximum required capacity and to allocate the proper number of channels in order to meet the GoS. GOS is typically given as the likelihood that a call is blocked, or the likelihood of a call experiencing a delay greater than a certain queuing time.
The traffic. intensity offered by each user is equal to the call request rate multiplied by the holding time. That is, each user generates a traffic intensity of Erlangs given by \(A_u =\lambda H \\\)
where H is the average duration of a call and $\lambda$ is the average number of call requests per unit time. For a system containing U users and an unspecified number of channels, the total offered traffic intensity A, is given as \(A = U A_u \\\)
Furthermore, in a C channel trunked system, if the traffic is equally distributed among the channels, then the traffic intensity per channel, is given as \(A_c = U A_u /C \\\)
Note that the offered traffic is not necessarily the traffic which is carried by the trunked system, only that which is offered to the trunked system. When the offered traffic exceeds the maximum capacity of the system, the carried traffic becomes limited due to the limited capacity (i.e. limited number of channels).
The maximum possible carried traffic is the total number of channels, C, in Erlangs. The AMPS cellular system is designed for a GOS of $2\%$ blocking. This implies that the channel allocations for cell sites are designed so that 2 out of 100 calls will be blocked due to channel occupancy during the busiest hour.
There are two types of trunked systems which are commonly used. The first type offers no queuing for call requests. That is, for every user who requests service,
it is assumed there is no setup time and the user is given immediate access to a channel if one is available. If no channels are available, the requesting user is blocked without access and is free to try again later.
This type of trunking is called blocked calls cleared and assumes that calls arrive as determined by’ a Poisson distribution. Furthermore, it is assumed that there are an infinite number of users as well as the following: (a) there are memoryless arrivals of requests, implying that all users, including blocked users, may request a channel at any time; (b) the probability of a user occupying a channel is exponentially distributed, so that longer calls are less likely to occur as described by an exponential distribution; and (c) there are a finite number of channels available in
the trunking pool.
This is known as an M/M/m queue, and leads to the derivation of the Erlang B formula (also known as the blocked calls cleared formula).
The Erlang B formula determines the probability that a call is blocked and is a measure of the GOS for a trunked system which provides no queuing for blocked calls. The Erlang B formula is given by
\[P_b = \frac {\frac{A^K}{K!}}{ \Sigma_{n=0}^{K} A^n/n!} = GOS\]
Question: In a certain cellular system, an average subscriber places two calls per hour during a busy hour and the average holding time is 3 min. Each cell has $100$ channels. If the blocked calls are cleared, how many subscribers can be serviced by each cell at $2 \%$ GoS?
- Question: In the previous example, suppose that the channels have been divided into two groups of $50$ channels each. Each subscriber is assigned to a group and can be served only by that group. How many subscribers can be served by the two groups.